许多人或许没有听过《计算之书》的大名,但若提到它的作者斐波那契,应该多多少少会有些耳闻。
因为,数学上有个很有名的“斐波那契数列”。中国四大名著被过誉了吗?
所谓斐波那契数列,即:0,1,1,2,3,5,8,13……数列从第3项开始,每一项都等于前两项之和。
斐波那契数列是无穷无尽的,可以永远保持增长,——因为可以不断添加新数进去。
阶乘是用一个数乘以所有比它小的数(一直到1),它用“!”表示,所以5!就是5×4×3×2×1=120。
通常而言,阶乘都是用来表示非常大的数,比如:20!有19位;100!有158位。
而且,阶乘一般用来表示一串数字(或者其他东西)有多少种排列,例如,有5种不同颜色的筹码,就有120种不同的摆放方式;有20种不同颜色的筹码,那么就有2,432,902,008,176,640,000种不同的摆放方式。
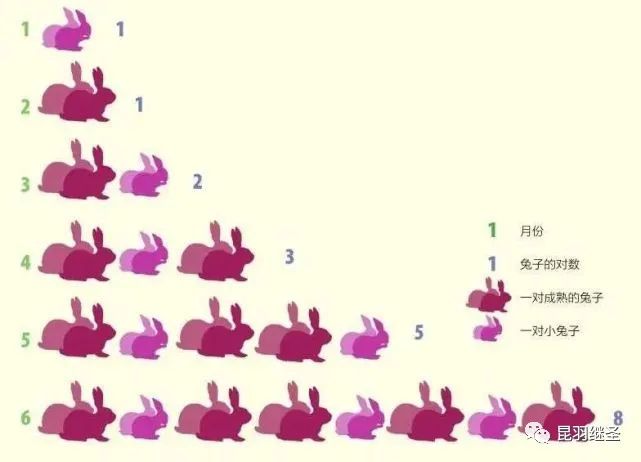
斐波那契数列运用在兔子繁殖问题中:
最开始有一对小兔子,一个月后成熟。
第二个月,母兔妊娠,第三个月,生一对小兔。
小兔也花一个月成熟,然后,如同它们的父母,从第三个月开始每月生一对小兔。
斐波那契发现每月的兔子数都是前两个月的数量之和。西方十大数学天才神话逐一破灭:对数之父纳皮尔神父也露出了马脚,竟是为哥白尼、开普勒、第谷而生,发明小数点、潜艇、坦克……
好了,大致了解了何谓斐波那契数列后,我们来看看斐波那契这位大神在其大作《计算之书》中提到的斐波那契数列长得什么样。

喏,瞧见了吧?
这就是《计算之书》页面边沿的斐波那契数列(阿拉伯数字),拉丁文版的(唯一的版本)。
试问,谁看得出来?
反正全凭西方一张嘴说呗,由中国南方方言语音结合汉语演化而来的拉丁文早已在18世纪就因为无法弥补的缺陷成为了一门死亡语言(Dead language),世界上能真正译读它的人根本就找不出几个来,要如何修改、描抹,那都是西方后世的事情。
恰如牛大神的万有引力:
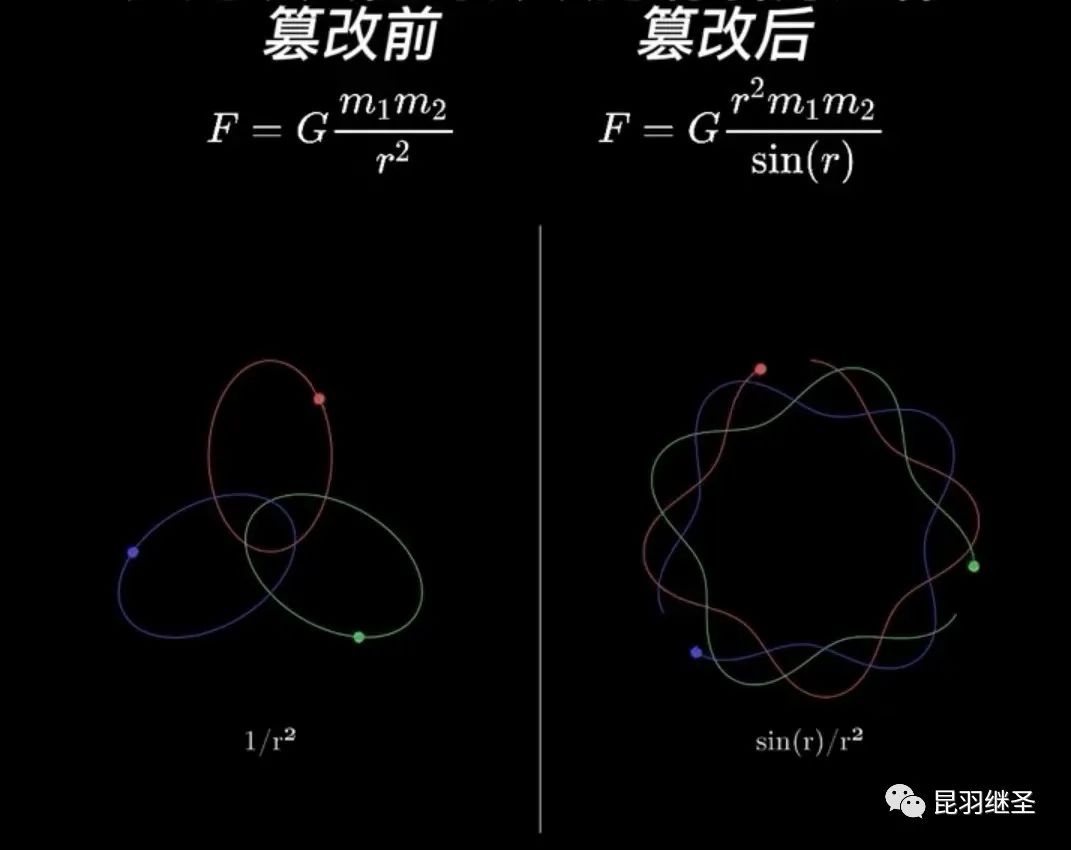
拉丁文版转成莫特的英文版后,从第一版到第三版,再到后世的版本,嗯,容错率提升了,“精度”也提升了不少。总之,虽然牛大神已经去世了很多年,但是万有引力与时俱进,依然无比正确、无比伟光正。

谁敢保证斐波那契与牛大神不是同样的故事呢?